Standard normalfördelning i matematikproblem

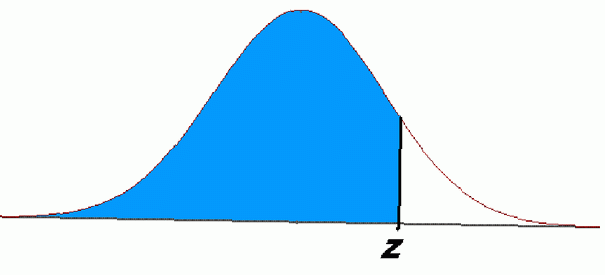
Den normala normalfördelningen, som är mer känd som klockkurvan, dyker upp på olika platser. Flera olika datakällor distribueras normalt. Som ett resultat av detta faktum kan vår kunskap om standardfördelningen användas i ett antal applikationer. Men vi behöver inte arbeta med en annan normalfördelning för varje applikation. Istället arbetar vi med en normalfördelning med ett medelvärde på 0 och en standardavvikelse på 1. Vi kommer att titta på några tillämpningar av denna distribution som alla är knutna till ett särskilt problem.

Exempel

Anta att vi får höra att höjden hos vuxna män i en viss region i världen normalt fördelas med ett medelvärde på 70 tum och en standardavvikelse på 2 tum.

1. Ungefär vilken andel vuxna män är högre än 73 tum?
2. Vilken andel vuxna män är mellan 72 och 73 tum?
3. Vilken höjd motsvarar den punkt där 20% av alla vuxna män är större än denna höjd?
4. Vilken höjd motsvarar den punkt där 20% av alla vuxna män är mindre än denna höjd?

lösningar

Innan du fortsätter, se till att sluta och gå igenom ditt arbete. Nedan följer en detaljerad förklaring av vart och ett av dessa problem:

1. Vi använder vår z-poängformel för att konvertera 73 till en standardiserad poäng. Här beräknar vi (73 - 70) / 2 = 1,5. Så frågan blir: vad är området under den normala normalfördelningen för z större än 1,5? Konsultera vårt bord av z-poäng visar oss att 0,933 = 93,3% av distributionen av data är mindre än z = 1,5. Därför är 100% - 93,3% = 6,7% av vuxna män högre än 73 tum.
2. Här konverterar vi våra höjder till en standardiserad z-Göra. Vi har sett att 73 har a z poäng 1,5. De z-poängen 72 är (72 - 70) / 2 = 1. Därför letar vi efter området under normalfördelningen för 1<z < 1.5. A quick check of the normal distribution table shows that this proportion is 0.933 - 0.841 = 0.092 = 9.2%
3. Här vänds frågan från vad vi redan har övervägt. Nu tittar vi upp i vårt bord för att hitta en z-Göra Z^* som motsvarar ett område på 0,200 ovan. För användning i vår tabell noterar vi att det är där 0,800 är nedan. När vi tittar på bordet ser vi det z^* = 0,84. Vi måste nu konvertera detta z-poäng till en höjd. Eftersom 0,84 = (x - 70) / 2, betyder detta det x = 71,68 tum.
4. Vi kan använda symmetrin för normalfördelningen och spara oss själva besväret med att slå upp värdet z^*. Istället för z^* = 0,84, vi har -0,84 = (x - 70) / 2. Således x = 68,32 tum.

Området för det skuggade området till vänster om z i diagrammet ovan visar dessa problem. Dessa ekvationer representerar sannolikheter och har många tillämpningar i statistik och sannolikhet.