Betydelsen av ömsesidigt exklusivt i statistik

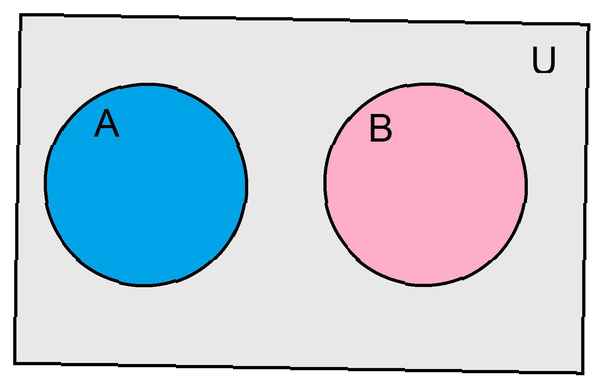
Det är troligt att två händelser sägs vara ömsesidigt exklusiva om och bara om händelserna inte har några delade resultat. Om vi ​​betraktar händelserna som uppsättningar, skulle vi säga att två händelser är ömsesidigt exklusiva när deras skärningspunkt är den tomma uppsättningen. Vi kan beteckna de händelserna EN och B är ömsesidigt exklusiva med formeln EN ∩ B = Ø. Liksom med många begrepp med sannolikhet kommer några exempel att hjälpa till att känna till denna definition.

Rullande tärningar

Anta att vi rullar två sexsidiga tärningar och lägger till antalet prickar som visas ovanpå tärningarna. Händelsen som består av "summan är jämn" är ömsesidigt utesluten från händelsen "summan är udda." Anledningen till detta är eftersom det inte finns något sätt att göra för ett nummer att vara jämnt och udda.

Nu kommer vi att utföra samma sannolikhetsexperiment att rulla två tärningar och lägga till de siffror som visas tillsammans. Den här gången kommer vi att överväga händelsen som består av att ha en udda summa och händelsen som består av att ha en summa större än nio. Dessa två händelser är inte ömsesidigt exklusiva.

Anledningen till varför är uppenbar när vi granskar händelsernas resultat. Den första händelsen har resultat på 3, 5, 7, 9 och 11. Den andra händelsen har resultat på 10, 11 och 12. Eftersom 11 är i båda dessa är händelserna inte ömsesidigt exklusiva.

Ritningskort

Vi illustrerar ytterligare med ett annat exempel. Anta att vi drar ett kort från ett standarddäck på 52 kort. Att rita ett hjärta är inte ömsesidigt uteslutande för händelse av att rita en kung. Detta beror på att det finns ett kort (hjärtan kungen) som dyker upp i båda dessa händelser.

Varför spelar det någon roll

Det finns tillfällen då det är mycket viktigt att avgöra om två händelser är ömsesidigt exklusiva eller inte. Att veta om två händelser är ömsesidigt exklusiva påverkar beräkningen av sannolikheten för att den ena eller den andra inträffar.

Gå tillbaka till kortexemplet. Om vi ​​drar ett kort från ett standardkort med 52 kort, är det troligt att vi har dragit ett hjärta eller en kung?

Först dela upp detta i enskilda händelser. För att hitta sannolikheten för att vi har dragit ett hjärta räknar vi först antalet hjärtan i däcket som 13 och delar sedan med det totala antalet kort. Detta innebär att sannolikheten för ett hjärta är 13/52.

För att hitta sannolikheten för att vi har dragit en kung börjar vi med att räkna det totala antalet kungar, vilket resulterar i fyra, och sedan dividerar med det totala antalet kort, vilket är 52. Sannolikheten för att vi har dragit en kung är 4/52.

Problemet är nu att hitta sannolikheten för att dra antingen en kung eller ett hjärta. Här måste vi vara försiktiga. Det är mycket frestande att helt enkelt lägga till sannolikheterna 13/52 och 4/52 tillsammans. Detta skulle inte vara korrekt eftersom de två händelserna inte är exklusivt. Kungen av hjärtan har räknats två gånger i dessa sannolikheter. För att motverka den dubbla räkningen måste vi subtrahera sannolikheten för att dra en kung och ett hjärta, som är 1/52. Därför är sannolikheten för att vi har dragit antingen en kung eller ett hjärta 16/52.

Andra användningar av ömsesidigt exklusivt

En formel känd som tilläggsregel ger ett alternativt sätt att lösa ett problem som ovan. Tilläggsregeln avser faktiskt ett par formler som är nära besläktade med varandra. Vi måste veta om våra händelser är ömsesidigt exklusiva för att veta vilken tilläggsformel som är lämplig att använda.