Kalkylblad om kombinationer och permutationer

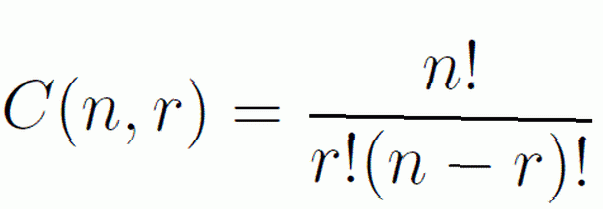
Permutationer och kombinationer är två begrepp som är relaterade till idéer med sannolikhet. Dessa två ämnen är mycket lika och är lätta att förväxla. I båda fallen börjar vi med en uppsättning som innehåller totalt n element. Då räknar vi r av dessa element. Hur vi räknar dessa element avgör om vi arbetar med en kombination eller med en permutation.

Beställning och arrangemang

De viktigaste sakerna att komma ihåg när man skiljer mellan kombinationer och permutationer har att göra med ordning och arrangemang. Permutationer handlar om situationer då ordningen att vi väljer objekt är viktig. Vi kan också tänka på detta som att det motsvarar idén att ordna föremål

I kombinationer handlar vi inte om vilken ordning vi valde våra objekt. Vi behöver bara detta koncept, och formlerna för kombinationer och permutationer för att lösa problem som rör detta ämne.

Öva problem

För att bli bra på något krävs det lite övning. Här är några övningsproblem med lösningar som hjälper dig att räta ut idéerna om permutationer och kombinationer. En version med svar finns här. När du har börjat med bara grundläggande beräkningar kan du använda vad du vet för att avgöra om en kombination eller permutation hänvisas till.

1. Använd formeln för permutationer för att beräkna P(5, 2).
2. Använd formeln för kombinationer för att beräkna C(5, 2).
3. Använd formeln för permutationer för att beräkna P(6, 6).
4. Använd formeln för kombinationer för att beräkna C(6, 6).
5. Använd formeln för permutationer för att beräkna P(100, 97).
6. Använd formeln för kombinationer för att beräkna C(100, 97).
7. Det är valtid på en gymnasium som har totalt 50 elever i juniorklassen. Hur många sätt kan en klasspresident, klass vice president, klasskassör och klasssekreterare väljas om varje student bara får ha ett kontor?
8. Samma klass på 50 studenter vill bilda en promkommitté. Hur många sätt kan en fyra personers utskott väljas från juniorklassen?
9. Om vi ​​vill bilda en grupp på fem studenter och vi har 20 att välja mellan, hur många sätt är det möjligt?
10. Hur många sätt kan vi ordna fyra bokstäver från ordet "dator" om upprepningar inte är tillåtna, och olika ordningar med samma bokstäver räknas som olika arrangemang?
11. Hur många sätt kan vi ordna fyra bokstäver från ordet "dator" om repetitioner inte är tillåtna, och olika ordningar med samma bokstäver räknas som samma arrangemang?
12. Hur många olika fyrsiffriga siffror är möjliga om vi kan välja siffror från 0 till 9 och alla siffror måste vara olika?
13. Om vi ​​får en låda med sju böcker, hur många sätt kan vi ordna tre av dem på en hylla?
14. Om vi ​​får en ruta som innehåller sju böcker, hur många sätt kan vi välja samlingar av tre av dem från rutan?