Nummeret Pi 3.14159265 ...

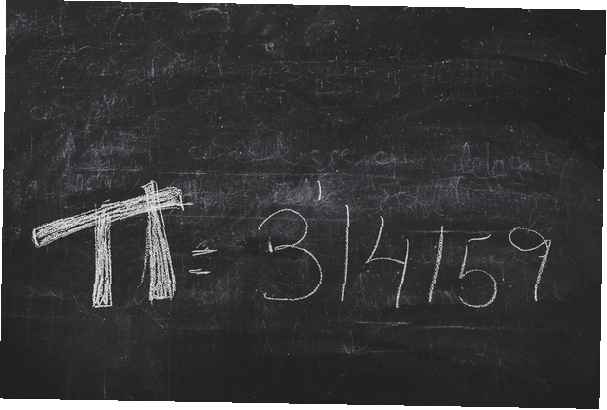
En av de mest använda konstanterna i hela matematiken är antalet pi, som betecknas med den grekiska bokstaven π. Begreppet pi har sitt ursprung i geometri, men detta antal har tillämpningar i hela matematiken och dyker upp i långtgående ämnen inklusive statistik och sannolikhet. Pi har till och med fått kulturellt erkännande och sin egen helgdag med firandet av Pi-dagens aktiviteter runt om i världen.

Värdet på Pi

Pi definieras som förhållandet mellan en cirkelns omkrets och dess diameter. Värdet på pi är något större än tre, vilket innebär att varje cirkel i universum har en omkrets med en längd som är lite mer än tre gånger dess diameter. Mer exakt har pi en decimalrepresentation som börjar 3.14159265 ... Detta är bara en del av decimalutvidgningen av pi.

Pi-fakta

Pi har många fascinerande och ovanliga funktioner, inklusive: 

• Pi är ett irrationellt verkligt tal. Detta betyder att pi inte kan uttryckas som en bråkdel a / b var en och b är båda heltal. Även om siffrorna 22/7 och 355/113 är användbara för att uppskatta pi, är ingen av dessa fraktioner det verkliga värdet på pi.
• Eftersom pi är ett irrationellt nummer upphör eller repeteras dess decimalalternativ aldrig. Det finns några frågor om denna decimalutvidgning, till exempel: Visas alla möjliga siffror i någon decimal i pi-decimalutvidgningen? Om varje möjlig sträng visas visas ditt mobilnummer någonstans i utvidgningen av pi (men så är alla andras).
• Pi är ett transcendentalt tal. Detta betyder att pi inte är nollet för ett polynom med heltalskoefficienter. Detta faktum är viktigt när man utforskar mer avancerade funktioner i pi.
• Pi är viktigt geometriskt, och inte bara för att det relaterar en cirkelns omkrets och diameter. Detta nummer visas också i formeln för en cirkelområde. Området med en radiecirkel r är EN = pi r². Antalet pi används i andra geometriska formler, såsom ytans yta och volym på en sfär, volym av en kon och volymen för en cylinder med en cirkulär bas.
• Pi visas när minst förväntat. För ett av många exempel på detta, överväg den oändliga summan 1 + 1/4 + 1/9 + 1/16 + 1/25 + ... Denna summa konvergerar till värdet pi²/ 6.

Pi i statistik och sannolikhet

Pi gör överraskande uppträdanden i hela matematiken, och några av dessa uppträdanden är i ämnen för sannolikhet och statistik. Formeln för den normala normalfördelningen, även känd som klockkurvan, innehåller numret pi som en konstant för normalisering. Med andra ord, genom att dela med ett uttryck som involverar pi kan du säga att området under kurvan är lika med ett. Pi är också en del av formlerna för andra sannolikhetsfördelningar.

En annan överraskande förekomst av pi med sannolikhet är ett hundra år gammalt nålkastande experiment. På 1700-talet ställde Georges-Louis Leclerc, Comte de Buffon en fråga om sannolikheten för att tappa nålar: Börja med ett golv med plankor av trä med en enhetlig bredd där linjerna mellan var och en av plankorna är parallella med varandra. Ta en nål med en längd kortare än avståndet mellan plankorna. Om du tappar en nål på golvet, är det troligt att det kommer att landa på en linje mellan två av träplankorna?

Som det visar sig är sannolikheten för att nålen landar på en linje mellan två plankor dubbelt så lång som nålen dividerad med längden mellan plankorna gånger pi.