De associerande och kommutativa egenskaperna

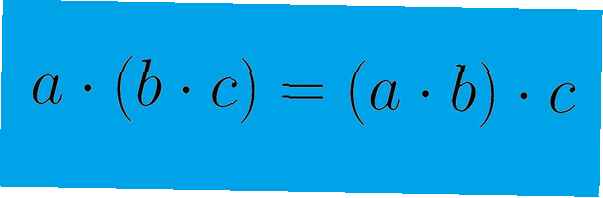
Det finns flera matematiska egenskaper som används i statistik och sannolikhet; två av dessa, de kommutativa och associativa egenskaperna, är i allmänhet förknippade med den grundläggande aritmetiken för heltal, rationaler och reella tal, även om de också dyker upp i mer avancerad matematik.

Dessa egenskaper - kommutativet och associativet - är mycket lika och kan enkelt blandas upp. Av den anledningen är det viktigt att förstå skillnaden mellan de två.

Den kommutativa egenskapen avser ordningen för vissa matematiska operationer. För en binär operation - en som endast involverar två element - kan detta visas med ekvationen a + b = b + a. Åtgärden är kommutativ eftersom orden på elementen inte påverkar resultatet av operationen. Den associerande egenskapen å andra sidan avser gruppering av element i en operation. Detta kan visas med ekvationen (a + b) + c = a + (b + c). Gruppering av elementen, som indikeras av parenteserna, påverkar inte resultatet av ekvationen. Observera att när den kommutativa egenskapen används, är element i en ekvation möblerat om. När den associerande egenskapen används är element bara omgrupperats.

Kommutativ egendom

Enkelt uttryckt anger den kommutativa egenskapen att faktorerna i en ekvation kan omarrangeras fritt utan att det påverkar utfallet av ekvationen. Den kommutativa egenskapen berör sig därför beställningen av operationer, inklusive tillägg och multiplikation av reella tal, heltal och rationella nummer.

Till exempel kan siffrorna 2, 3 och 5 läggas till i vilken ordning som helst utan att det påverkar slutresultatet:

2 + 3 + 5 = 10

3 + 2 + 5 = 10

5 + 3 + 2 = 10

Siffrorna kan också multipliceras i valfri ordning utan att det påverkar slutresultatet:

2 x 3 x 5 = 30

3 x 2 x 5 = 30

5 x 3 x 2 = 30

Subtraktion och uppdelning är emellertid inte operationer som kan vara kommuterande eftersom arbetsordningens ordning är viktig. De tre siffrorna ovan kan inte, till exempel subtraheras i någon ordning utan att påverka det slutliga värdet:

2 - 3 - 5 = -6

3 - 5 - 2 = -4

5 - 3 - 2 = 0