Den fotoelektriska effekten

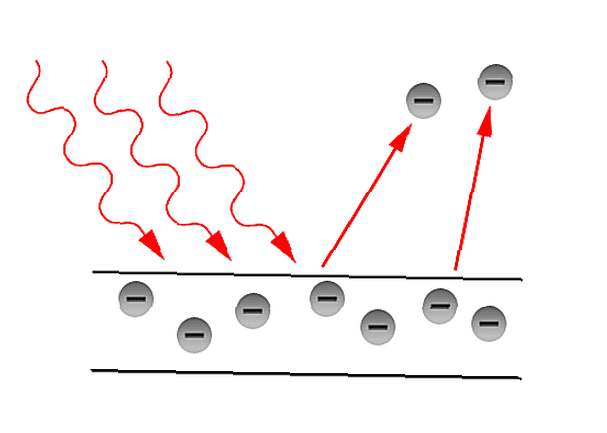
De fotoelektrisk effekt utgjorde en betydande utmaning för studien av optik under den senare delen av 1800-talet. Det utmanade klassisk vågteori av ljus, vilket var tidens rådande teori. Det var lösningen på detta fysikdilemma som katapulterade Einstein till framträdande inom fysiksamhället och slutligen fick honom Nobelpriset 1921.

Vad är den fotoelektriska effekten?

Annalen der Physik

När en ljuskälla (eller mer generellt elektromagnetisk strålning) inträffar på en metallisk yta, kan ytan avge elektroner. Elektroner som släpps ut på detta sätt kallas fotoelektroner (även om de fortfarande bara är elektroner). Detta visas på bilden till höger.

Ställa in den fotoelektriska effekten

Genom att administrera en negativ spänningspotential (den svarta rutan på bilden) till samlaren tar det mer energi för elektronerna att slutföra resan och initiera strömmen. Den punkt där inga elektroner kommer till kollektorn kallas stoppande potential V_s, och kan användas för att bestämma den maximala kinetiska energin K_max av elektronerna (som har elektronisk laddning e) genom att använda följande ekvation:

K_max = eV_s

Klassisk vågförklaring

Iwork-funktion phiPhi

Tre huvudsakliga förutsägelser kommer från denna klassiska förklaring:

1. Strålningens intensitet bör ha ett proportionellt förhållande till den resulterande maximala kinetiska energin.
2. Den fotoelektriska effekten bör uppstå för alla ljus, oavsett frekvens eller våglängd.
3. Det bör finnas en fördröjning i sekvensordningen mellan strålningens kontakt med metallen och den initiala frisättningen av fotoelektroner.

Det experimentella resultatet

1. Ljuskällans intensitet påverkade inte fotoelektronernas maximala kinetiska energi.
2. Under en viss frekvens uppträder den fotoelektriska effekten inte alls.
3. Det finns ingen betydande försening (mindre än 10^-9 s) mellan ljuskällans aktivering och emissionen av de första fotoelektronerna.

Som ni kan säga är dessa tre resultat precis motsatsen till vågteorins förutsägelser. Inte bara det, utan de är alla tre helt intuitiva. Varför skulle lågfrekvent ljus inte utlösa den fotoelektriska effekten, eftersom det fortfarande bär energi? Hur släpper fotoelektronerna så snabbt? Och kanske märkligast, varför resulterar det inte i mer energiska elektronutsläpp att lägga till mer intensitet? Varför misslyckas vågteorin så fullständigt i detta fall när den fungerar så bra i så många andra situationer

Einsteins underbara år

Albert Einstein Annalen der Physik

Med utgångspunkt i Max Plancks svartkroppsstrålningsteori föreslog Einstein att strålningsenergi inte kontinuerligt distribueras över vågfronten utan istället lokaliseras i små buntar (senare kallade fotoner). Fotonens energi skulle vara associerad med dess frekvens (ν), genom en proportionalitetskonstant känd som Plancks konstant (h) eller omväxlande med våglängden (λ) och ljusets hastighet (c):

E = hv = hc / λ

eller momentumekvationen: p = h / λ