Kalkylblad för Chebyshevs ojämlikhet

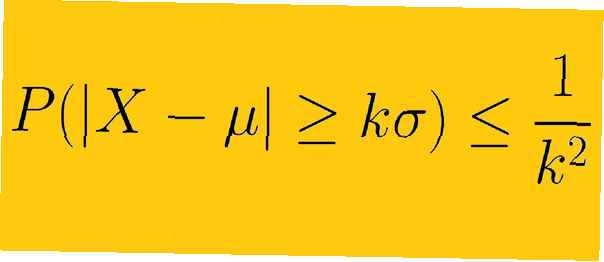
Chebysjevs ojämlikhet säger att minst 1 -1 /K² av data från ett prov måste falla inom K standardavvikelser från medelvärdet, var K är något positivt reellt antal större än ett. Detta betyder att vi inte behöver veta formen för distributionen av våra data. Med endast medel- och standardavvikelsen kan vi bestämma mängden data som ett visst antal standardavvikelser från medelvärdet har.

Följande är några problem att öva med att använda ojämlikheten.

Exempel 1

En klass av andra klassare har en medelhöjd på fem fot med en standardavvikelse på en tum. Åtminstone vilken procent av klassen måste vara mellan 4'10 "och 5'2"?

Lösning

Höjderna som anges i området ovan ligger inom två standardavvikelser från medelhöjden på fem fot. Chebysjevs ojämlikhet säger att minst 1 - 1/2² = 3/4 = 75% av klassen ligger inom det givna höjdområdet.

Exempel 2

Datorer från ett visst företag har visat sig vara i genomsnitt i tre år utan hårdvarufel, med en standardavvikelse på två månader. Åtminstone vilken procent av datorerna varar mellan 31 månader och 41 månader?

Lösning

Den genomsnittliga livslängden på tre år motsvarar 36 månader. Tiderna på 31 månader till 41 månader är vardera 5/2 = 2,5 standardavvikelser från medelvärdet. Genom Chebysjevs ojämlikhet, minst 1 - 1 / (2.5) 6² = 84% av datorerna varar från 31 månader till 41 månader.

Exempel 3

Bakterier i en kultur lever i en genomsnittlig tid på tre timmar med en standardavvikelse på 10 minuter. Åtminstone vilken del av bakterierna lever mellan två och fyra timmar?

Lösning

Två och fyra timmar är vardera en timme bort från medelvärdet. En timme motsvarar sex standardavvikelser. Så minst 1 - 1/6² = 35/36 = 97% av bakterierna lever mellan två och fyra timmar.

Exempel 4

Vilket är det minsta antalet standardavvikelser från medelvärdet som vi måste gå om vi vill se till att vi har minst 50% av uppgifterna för en distribution?

Lösning

Här använder vi Chebysjevs ojämlikhet och arbetar bakåt. Vi vill ha 50% = 0,50 = 1/2 = 1 - 1 /K². Målet är att använda algebra för att lösa för K.

Vi ser att 1/2 = 1 /K². Korsa multiplicera och se att 2 =K². Vi tar kvadratroten på båda sidor, och sedan K är ett antal standardavvikelser, vi ignorerar den negativa lösningen på ekvationen. Detta visar det K är lika med kvadratroten av två. Så minst 50% av uppgifterna ligger inom ungefär 1,4 standardavvikelser från medelvärdet.

Exempel 5

Bussrutt nr 25 tar en genomsnittlig tid på 50 minuter med en standardavvikelse på 2 minuter. En PR-affisch för detta bussystem säger att "95% av tiden bussrutt # 25 varar från ____ till _____ minuter." Vilka nummer skulle du fylla i ämnena med?