Z-Scores-arbetsblad

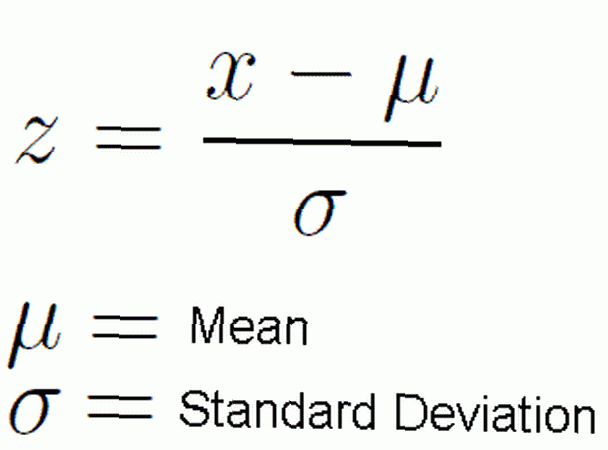
En standardtyp av problem från en introduktionskurs för statistik är att beräkna z-poäng av ett visst värde. Detta är en mycket grundläggande beräkning, men är en som är ganska viktig. Anledningen till detta är att det tillåter oss att vada genom det oändliga antalet normala fördelningar. Dessa normala fördelningar kan ha något medelvärde eller någon positiv standardavvikelse.

De z-poängformel börjar med det oändliga antalet distributioner och låter oss bara arbeta med den normala normalfördelningen. Istället för att arbeta med en annan normalfördelning för varje applikation som vi stöter på behöver vi bara arbeta med en speciell normalfördelning. Normal normalfördelning är denna väl studerade distribution.  

Förklaring av processen

Vi antar att vi arbetar i en miljö där våra data normalt distribueras. Vi antar också att vi får medelvärdet och standardavvikelsen för den normala fördelningen som vi arbetar med. Genom att använda z-poängformeln: z = (x - μ) / σ kan vi konvertera valfri distribution till den normala normalfördelningen. Här är den grekiska bokstaven μ medelvärdet och σ standardavvikelsen. 

Normal normalfördelning är en speciell normalfördelning. Det har ett medelvärde på 0 och dess standardavvikelse är lika med 1.

Z-poängproblem

Alla följande problem använder formeln z-poäng. Alla dessa övningsproblem innebär att man hittar en z-poäng från den information som ges. Se om du kan ta reda på hur du använder denna formel.

1. Poäng på ett historiktest har i genomsnitt 80 med standardavvikelse på 6. Vad är? z-poäng för en student som fick 75 på testet?
2. Vikten av chokladkakor från en viss chokladfabrik har ett medelvärde på 8 uns med standardavvikelse på 0,1 gram. Vad är z-poäng motsvarande en vikt av 8,17 ounce?
3. Böcker i biblioteket har visat sig ha en genomsnittlig längd på 350 sidor med standardavvikelse på 100 sidor. Vad är z-poäng motsvarande en bok med längd 80 sidor?
4. Temperaturen registreras på 60 flygplatser i en region. Medeltemperaturen är 67 grader Fahrenheit med standardavvikelse på 5 grader. Vad är z-poäng för en temperatur på 68 grader?
5. En grupp vänner jämför vad de fick när de lurade eller behandlade. De finner att det genomsnittliga antalet mottagna bitar av godis är 43 med standardavvikelse på 2. Vad är det? z-poäng motsvarande 20 godisbitar?
6. Den genomsnittliga tillväxten av tjockleken på träd i en skog har visat sig vara 0,5 cm / år med en standardavvikelse på 0,1 cm / år. Vad är z-poäng motsvarande 1 cm / år?
7. Ett särskilt benben för dinosauriefossiler har en medellängd på 5 fot med standardavvikelse på 3 tum. Vad är z-poäng som motsvarar en längd på 62 tum?

När du har räknat ut dessa problem måste du kontrollera ditt arbete. Eller kanske om du sitter fast på vad du ska göra. Lösningar med några förklaringar finns här.