Vad är sannolikhetsaxiomer?

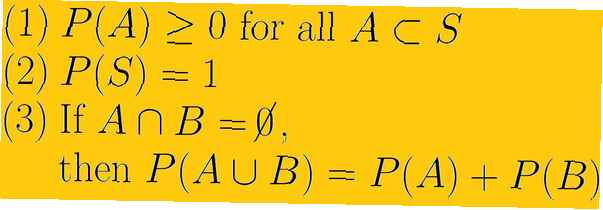
En strategi inom matematik är att börja med några uttalanden och sedan bygga upp mer matematik från dessa uttalanden. De första uttalandena är kända som axiomer. En axiom är vanligtvis något som är matematiskt självklart. Från en relativt kort lista över axiomer används deduktiv logik för att bevisa andra påståenden, kallade teorem eller förslag.

Matematikområdet som kallas sannolikhet är inte annorlunda. Sannolikheten kan minskas till tre axiomer. Detta gjordes först av matematikern Andrei Kolmogorov. Den handfull axiomer som är underliggande sannolikhet kan användas för att härleda alla möjliga resultat. Men vad är dessa sannolikhetsaxiomer?

Definitioner och förberedelser

För att förstå axiomerna för sannolikhet måste vi först diskutera några grundläggande definitioner. Vi antar att vi har en uppsättning resultat som kallas provutrymmet S. Detta exempelutrymme kan betraktas som den universella uppsättningen för den situation som vi studerar. Exempelutrymmet består av undergrupper som kallas händelser E₁, E₂,... , E_n. 

Vi antar också att det finns ett sätt att tilldela en sannolikhet till varje händelse E. Detta kan betraktas som en funktion som har en uppsättning för en ingång och ett verkligt tal som en utgång. Sannolikheten för händelsen E betecknas med P(E).

Axiom One

Den första axiom av sannolikhet är att sannolikheten för någon händelse är ett icke-negativt verkligt tal. Detta betyder att den minsta som en sannolikhet någonsin kan vara är noll och att den inte kan vara oändlig. Uppsättningen siffror som vi kan använda är verkliga siffror. Detta hänvisar till både rationella nummer, även kända som bråk, och irrationella nummer som inte kan skrivas som bråk.

En sak att notera är att detta axiom inte säger något om hur stor sannolikheten för en händelse kan vara. Axiom eliminerar inte risken för negativa sannolikheter. Det återspeglar uppfattningen att minsta sannolikhet, reserverad för omöjliga händelser, är noll.

Axiom Two

Den andra sannolikheten är att sannolikheten för hela provutrymmet är en. Symboliskt skriver vi P(S) = 1. Implicit i detta axiom är uppfattningen att provutrymmet är allt möjligt för vårt sannolikhetsexperiment och att det inte finns några händelser utanför provutrymmet.

I sig själv sätter detta axiom inte en övre gräns för sannolikheten för händelser som inte är hela samplingsutrymmet. Det återspeglar att något med absolut säkerhet har en sannolikhet på 100%.

Axiom Three

Det tredje sannolikhetsmomentet handlar om ömsesidigt exklusiva händelser. Om E₁ och E₂ är ömsesidigt exklusiva, vilket innebär att de har en tom korsning och vi använder U för att beteckna unionen P(E₁ U E₂ ) = P(E₁) + P(E₂).

Axiomen täcker faktiskt situationen med flera (till och med oändligt oändliga) händelser, vars alla par är ömsesidigt exklusiva. Så länge detta inträffar är sannolikheten för föreningen av händelserna densamma som summan av sannolikheterna:

P(E₁ U E₂ U U E_n ) = P(E₁) + P(E₂) + ... + E_n

Även om denna tredje axiom kanske inte verkar så användbar, kommer vi att se att i kombination med de andra två axiomerna är den verkligen ganska kraftfull.

Axiom-applikationer

De tre axiomerna sätter en övre gräns för sannolikheten för någon händelse. Vi anger komplementet till evenemanget E förbi E^C. Från uppsättningsteori, E och E^C har en tom korsning och är ömsesidigt exklusiva. vidare E U E^C = S, hela provutrymmet.

Dessa fakta, i kombination med axiomerna ger oss: