Parade data i statistik

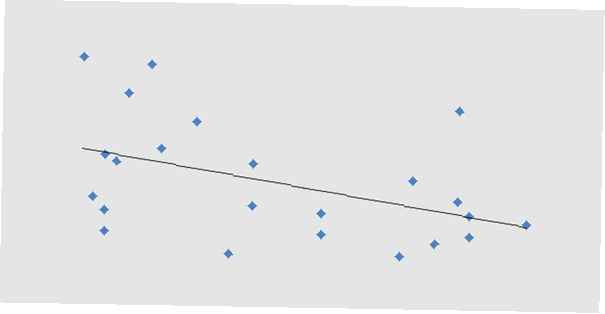
Parade data i statistik, ofta kallad ordnade par, hänvisar till två variabler hos individerna i en population som är länkade ihop för att bestämma sambandet mellan dem. För att en datauppsättning ska betraktas som ihopkopplade data måste båda dessa datavärden bifogas eller länkas till varandra och inte betraktas separat.

Idén med parade data kontrasteras med den vanliga kopplingen av ett nummer till varje datapunkt som i andra kvantitativa datamängder genom att varje individuell datapunkt är associerad med två siffror, vilket ger en graf som gör det möjligt för statistiker att observera förhållandet mellan dessa variabler i en befolkning.

Denna metod med parade data används när en studie hoppas kunna jämföra två variabler hos individer i befolkningen för att dra någon sorts slutsats om den observerade korrelationen. När man observerar dessa datapunkter är parningens ordning viktig eftersom det första talet är ett mått på en sak medan den andra är ett mått på något helt annat.

Exempel på ihopkopplade data

För att se ett exempel på ihopkopplade data, antar att en lärare räknar antalet läxuppgifter som varje elev lade in för en viss enhet och koppla sedan in detta nummer med varje elevs procenttal på enhetstestet. Paren är som följer:

• En person som slutförde 10 uppdrag tjänade 95% på sitt test. (10, 95%)
• En person som slutförde 5 uppdrag tjänade 80% på sitt test. (5, 80%)
• En person som slutförde 9 uppdrag tjänade 85% på sitt test. (9, 85%)
• En person som slutförde 2 uppdrag tjänade 50% på sitt test. (2, 50%)
• En person som slutförde 5 uppdrag tjänade 60% på sitt test. (5, 60%)
• En person som slutförde 3 uppdrag tjänade 70% på sitt test. (3, 70%)

I var och en av dessa uppsättningar av parade data kan vi se att antalet uppdrag alltid kommer först i det beställda paret medan den procentuella andelen som uppnås på testet kommer på andra plats, som det ses i första instansen av (10, 95%).

Medan en statistisk analys av dessa data också kan användas för att beräkna det genomsnittliga antal läxuppgifter som har genomförts eller det genomsnittliga testresultatet, kan det finnas andra frågor att ställa om uppgifterna. I det här fallet vill läraren veta om det finns något samband mellan antalet läxuppgifter som är inställda och prestanda i testet, och läraren skulle behöva hålla data ihopkopplade för att kunna besvara denna fråga.

Analysera ihopkopplade data

De statistiska teknikerna för korrelation och regression används för att analysera parade data varvid korrelationskoefficienten kvantifierar hur nära data ligger längs en rak linje och mäter styrkan hos den linjära relationen.

Återgång används å andra sidan för flera applikationer, inklusive att bestämma vilken linje som passar bäst för vår uppsättning data. Denna rad kan sedan i sin tur användas för att uppskatta eller förutsäga y värden för värden på x som inte ingick i vår ursprungliga datauppsättning.

Det finns en speciell typ av graf som är särskilt väl lämpad för parade data som kallas en spridplot. I denna typ av graf representerar en koordinataxel en kvantitet av de parade data medan den andra koordinataxeln representerar den andra kvantiteten av de parade data.

En spridningsdiagram för ovanstående data skulle ha x-axeln att beteckna antalet tilldelade inställningar medan y-axeln skulle beteckna poängen på enhetstestet.